Extracting the collective wisdom in probabilistic judgments
Cem Peker
Erasmus School of Economics, Erasmus University Rotterdam
Wisdom of Crowds?
An event from Metaculus.com (a community forecasting platform)
Individuals disagree, how should we combine judgments?
Wisdom of Crowds?
An event from Metaculus.com (a community forecasting platform)
Individuals disagree, how should we combine judgments?
Individuals disagree, how should we combine judgments?
Simple averaging is hard to beat (Clemen, 1989; Soll, 2009)
Problem: Shared information
Problem: Shared information
"Linear aggregation problem" (Palley and Soll, 2019; Palley and Satopaa, 2022)
$N$ risk-neutral agents, predict unknown probability $\theta$
Common prior + IID unbiased signal(s)
$$ \text{prediction: }x_i = (1-\omega) \,\, \color{orange}{s} \, + \, \omega \,\, \color{orange}{t_i}$$
Simple average of predictions?
"Linear aggregation problem" (Palley and Soll, 2019; Palley and Satopaa, 2022)
$Y \in \{0,1\}$: outcome of the event, $\theta = P(Y=1)$
Common prior on $\theta$: $Beta(m s, m(1-s))$
$t_i$: average of $\ell$ independent realizations of $Y$
Posterior belief: $Beta(ms + \ell t_i, m(1-s) + \ell(1-t_i))$ with $$E[\theta | s,t_i] = \frac{m}{m+\ell} s + \frac{\ell}{m+\ell} t_i$$
Let $\omega = \ell/(m+\ell) \,$ and $\, E[\theta | s,t_i] = (1-\omega) \, s + \omega \, t_i$
Simple average of predictions?
$$ \bar{x} = (1-\omega) \,\, \color{orange}{s} \, + \, \omega \,\, \color{orange}{\frac{1}{N} \sum_{i=1}^N t_i} $$
Then, \begin{align} \lim_{N \to \infty} \bar{x} &= (1-\omega) \,\, \color{orange}{s} + \omega \,\, \color{orange}{\theta} \neq \theta \quad \text{ for } \quad s \neq \theta \end{align}
Shared-information problem (Palley and Soll, 2019; Palley and Satopaa, 2022)
A robust aggregation method?
This paper develops the Surprising Overshoot (SO) algorithm.
Elicits and uses meta-beliefs
Prelec et al. (2017), Palley and Soll (2019), Wilkening et al. (2021), Palley and Satopaa (2022)
Meta-belief example:
What is the probability of a ceasefire in Ukraine before 2023?
(prediction)
What is the average probability estimated by the other experts?
(meta-prediction)
Linear predictions and meta-predictions
$$ \text{prediction: } \quad x_i = \underbrace{(1-\omega) \,\, \color{orange}{s}}_\text{shared} \, + \, \underbrace{\omega \,\, \color{orange}{t_i}}_\text{private}$$
$$ \text{meta-prediction: } \quad z_i = (1-\omega) \,\, \color{orange}{s} \, + \, \omega \underbrace{E\left[ \frac{1}{N-1} \sum\limits_{j \neq i} t_j \, \middle\vert \, s,t_i \right]}_\text{Expectation on avg signal of others} \\ $$
For $N \to \infty$...
$$z_i > \bar{x} \iff x_i > \theta$$
Overestimate $\bar{x}$ in meta-prediction $\iff$ Overestimate $\theta$ in prediction
SO estimator:
1. Calculate $q=$ {% of $z_i < \bar{x}$ in the sample}
2. Pick sample quantile of predictions at $q$
Suppose expert $i$'s meta-prediction overshoots average prediction
$\displaystyle z_i > \bar{x} $
$\displaystyle \color{orange}{(1-\omega) s} + \omega \underbrace{E\left[ \frac{1}{N-1} \sum\limits_{j \neq i} t_j \, \middle\vert \, s,t_i \right]}_\text{Expectation on avg signal of others} > \color{orange}{(1-\omega) s} + \omega \underbrace{\frac{1}{N} \sum_{i=1}^N t_i}_\text{avg signal}$
$\displaystyle \underbrace{E\left[ \theta | s,t_i \right]}_\text{expert $i$'s prediction ($x_i$)} > \underbrace{\frac{1}{N} \sum_{i=1}^N t_i}_\text{converges to $\theta$ for $N \to \infty$}$
SO estimator
Improvement in accuracy when...
1. $N$ is not very small.
2. High disagreement in predictions (difficult questions).
1. $N$ is not very small.
Evidence using Study 1 from Palley and Soll (2019).
Subjects guess Prob(Heads) of a biased two-sided coin.
48 coins, 685 subjects
Comparative analysis of forecast errors (SO vs benchmarks)

1. $N$ is not very small.
Average forecast errors, bootstrap crowds of size {10,20,...,100}.
SO estimator has the lowest error in moderate to large samples.
Minimal Pivoting (Palley and Soll, 2019), Knowledge Weighting (Palley and Satopaa, 2022), Meta-Probability Weighting (Martinie et al., 2020)
1. $N$ is not very small.
Average forecast errors, bootstrap crowds of size {10,20,...,100}.
SO estimator has the lowest error in moderate to large samples.
Intuition: Sample quantile converges as $N \to \infty$
Minimal Pivoting (Palley and Soll, 2019), Knowledge Weighting (Palley and Satopaa, 2022), Meta-Probability Weighting (Martinie et al., 2020)
Why does the SO algorithm work?
Positive (Negative) bias in $\bar{x} \to \bar{x}$ should be higher (lower) than the SO estimate
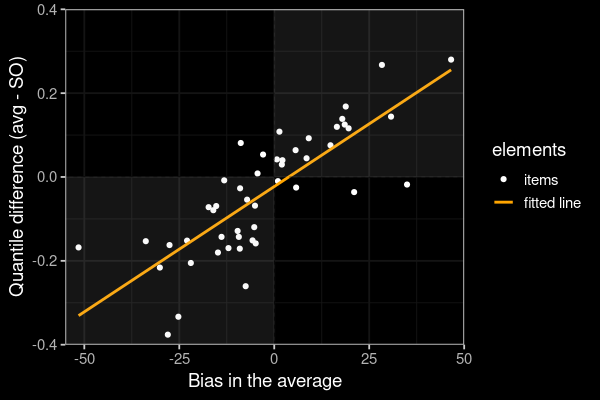
SO estimator
Higher improvement in accuracy when...
1. $N$ is not very small. ✓
2. High disagreement among experts (difficult questions).
2. High disagreement in predictions (difficult questions).
Evidence using data from Wilkening et al. (2021)
"General Knowledge"
"Herbivores eat both plants and animals" (True or False?)
"State Capital"
"Los Angeles is the capital city of California" (True or False?)
- What is the probability that the statement is true?
- What is the average probability estimated by the others?
500 questions, 459 subjects
50 questions, 89 subjects
2. High disagreement in predictions (difficult questions).
Analysis:
Categorize questions according to std dev in predictions (= disagreement).
Bootstrap samples of questions in each category
Brier scores, 95% Bootstrap conf. intervals (SO vs. each benchmark).
2. High disagreement in predictions (difficult questions).
Box plots: 95% confidence intervals (SO score - benchmark score)
SO algorithm is more accurate than alternatives in high-disagreement questions.
Intuition: Higher dispersion $\implies$ distinct quantiles
2. High disagreement in predictions (difficult questions).
Box plots: 95% confidence intervals (SO score - benchmark score)
SO algorithm is more accurate than alternatives in high-disagreement questions.
Intuition: Higher dispersion $\to$ distinct quantiles
SO estimator
Higher improvement in accuracy when...
1. $N$ is not very small. ✓
2. High disagreement in predictions (difficult questions). ✓
★ Effective in moderate to large samples & difficult questions.
Questions?
